学ぶことで、複雑に見えることが、シンプルであることがわかる。
この言葉は、私たちが何か新しいことを学び始めたときに経験する典型的な学習プロセスを表しています。
新しいトピックや概念に初めて触れると、それが複雑で理解しづらいと感じることがよくあります。
しかし、時間と努力をかけて学習を進めると、最初は複雑に見えたものが実はシンプルで理解しやすいものであることがわかってきます。
このプロセスをより具体的な例を通じて探求してみましょう。
例1: 数学の方程式
まず、数学の世界でこのプロセスを考えてみましょう。
方程式を解くことは初学者にとって複雑に思えるかもしれません。
例えば、以下のような方程式を考えてみましょう。

3x + 2 = 8
初めて見たとき、xの値を求めるのは難しそうに思えます。
しかし、学習を進めると、方程式を解くための基本的なステップを学びます。
両辺から2を引く:3x = 8 – 2 → 3x = 6
両辺を3で割る:3x / 3 = 6 / 3 → x = 2
初めての方程式は複雑に見えましたが、基本的な操作を適用することで、xの値が2であることがシンプルにわかります。
つまり、数学の方程式も初めは複雑に見えますが、基本的なルールやスキルを習得することでシンプルに解決できるものです。
例2: プログラミング言語
次に、プログラミングの世界での学習プロセスを考えてみましょう。
プログラミングは初めて触れたとき、コードが一連の英数字や記号で構成されており、理解しづらいと感じるかもしれません。
例として、Pythonプログラミング言語での条件文を考えてみましょう。
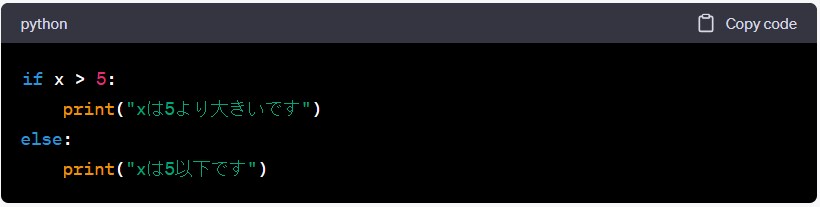
if x > 5:
print(“xは5より大きいです”)
else:
print(“xは5以下です”)
初めて見ると、このコードがどのように動作するのか理解するのは難しいかもしれません。
しかし、プログラミングを学習すると、条件文の基本的な原則を理解することができます。
if 文は条件を評価し、条件が真であれば最初のブロックを実行します。
else 文は条件が偽の場合に実行されるブロックを指定します。
したがって、このコードは「xが5より大きい場合は ‘xは5より大きいです’ を表示し、それ以外の場合は ‘xは5以下です’ を表示します」というシンプルなロジックを持っています。
例3: 科学的な理論
さらに、科学の分野でもこのプロセスが顕著に現れます。
例として、アインシュタインの特殊相対性理論を考えてみましょう。
この理論は、初めて聞いたときには非常に複雑に思えるかもしれません。
しかし、学習を進めると、特殊相対性理論はE=mc²(エネルギーは質量と光の速度の二乗に比例する)という単純な数式に基づいており、これが理論の中心となります。
この数式は非常にシンプルでありながら、私たちの物理学の理解を根本的に変えました。
まとめ
この言葉は、学習のプロセスにおける複雑性とシンプルさの対比を示唆しています。
初めて新しいトピックや概念に触れたとき、それが複雑に見えることはよくありますが、学習を進めるとその複雑性は基本的な原則やパターンに還元され、シンプルで理解しやすいものとなります。
このプロセスを通じて、私たちは知識と理解を深め、問題解決能力を高めることができます。
学習において、最初の複雑性に立ち向かうことは重要です。
しかし、それを乗り越え、基本的な原則を理解し、知識を構築することで、私たちは新しい分野やスキルを習得し、成長することができます。
この言葉は、学習の喜びと成長の過程を象徴しており、私たちに学び続ける意欲を与えてくれます。


